Читати книгу - "Пояснюючи світ"
Шрифт:
Інтервал:
Добавити в закладку:
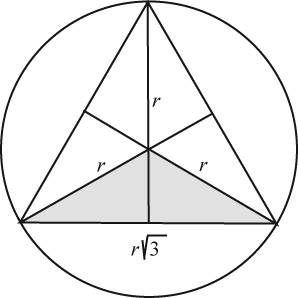
Рис. 15. Еліптичний рух планет. Формою орбіти тут є еліпс, який (як і на рис. 12) має еліптичність 0,8 – набагато більшу за еліптичність будь-якої планетної орбіти в Сонячній системі. Відрізки, позначені r+ та r–, з’єднують Сонце з планетою та порожнім фокусом еліпса відповідно.
Уважний читач помітить, що це дуже подібне до того, що описують закони Кеплера. Звісно, ролі Сонця та Землі в системах Птолемея та Коперника протилежні, але порожній фокус еліпса в теорії Кеплера відіграє ту саму роль, що й еквант у Птолемеєвій астрономії, а другий закон Кеплера пояснює, чому введення екванта добре працювало в поясненні видимого руху планет.
З деяких причин, хоч Птолемей і запровадив ексцентр, щоб описати рух Сонця навколо Землі, він не використовував еквант у цьому разі. Якщо зважити на цей кінцевий еквант (а також ввести деякі додаткові епіцикли, щоб урахувати значне відхилення форми орбіти Меркурія від форми кола), то теорія Птолемея могла б дуже добре пояснювати видимі рухи планет.
Ось доведення рівняння (1). Визначимо θ як кут між головною віссю еліпса та відрізком від Сонця до планети і пригадаймо, що ϕ ми визначили як кут між головною віссю та відрізком від порожнього фокуса до планети. Як і в технічній примітці 18, визначимо r+ та r– як довжини цих відрізків, тобто відстані від Сонця до планети та від порожнього фокуса до планети відповідно, задані (згідно з цією приміткою) рівнянням:
(2)де x – горизонтальна координата точки на еліпсі, тобто відстань від цієї точки до прямої, що перетинає еліпс уздовж його малої осі.
Косинус кута (позначений як cos) визначають у тригонометрії, розглядаючи прямокутний трикутник із таким кутом при одній із вершин; косинус кута є відношенням катета, прилеглого до цього кута, до гіпотенузи трикутника. Отже, за рис. 15 отримуємо:
. (3)Ми можемо розв’язати рівняння з лівого боку для x:
(4)Підставимо цей результат у формулу для cos ϕ, пов’язавши кути θ та ϕ:
(5)Оскільки рівність справедлива за будь-яких значень θ, то в разі внесення будь-яких змін до θ зміна в лівій частині рівності має дорівнювати зміні у правій його частині. Припустімо, ми вносимо до θ нескінченно малу зміну δθ (дельта тета). Щоб обчислити зміну ϕ, використовуємо правило: якщо будь-який кут α (наприклад, θ або ϕ) змінюється на величину δα (дельта альфа), то зміна cosα дорівнює −(δα/R) sinα. Крім того, якщо будь-яка величина f, як, наприклад, знаменник у рівнянні (5), змінюється на нескінченно малу величину δf, то зміна 1/f дорівнює −δf/f 2. Отже, урівнювання змін з обох боків рівняння (5) дає:
(6)Тепер нам потрібна формула для співвідношення sinϕ та sinθ. З цією метою зауважмо з рис. 15, що вертикальна координата y точки на еліпсі задана як y = r+ sinθ, а також y = r– sinϕ. Тому, скоротивши y, отримуємо:
(7)Використовуючи це в рівнянні (6), отримуємо:
(8)То яку ж площу покриває відрізок від Сонця до планети, коли кут θ змінюється на δθ? Якщо ми вимірюємо кути у градусах, тоді це площа рівнобедреного трикутника з двома сторонами, що дорівнюють r+, і третьою стороною, що дорівнює довжині дуги 2πr+ × δθ/360° окружності 2πr+ кола радіусом r+. Ця площа дорівнює:
(9)Знак мінус тут поставлено, бо ми хочемо, щоб величина δА залишалася додатною за зростання ϕ; але з огляду на те, як ми визначили ці кути, ϕ зростає, коли зменшується θ, тому δϕ є додатною величиною за негативної δθ. Отже, рівняння (8) можна записати так:
(10)Взявши δА та δϕ як площу та кут, які покриваються за нескінченнонескінченно малий часовий проміжок δt, і поділивши рівняння (10) на δt, ми знаходимо відповідне співвідношення між покритими площами та кутами:
(11)Наразі маємо точну рівність. Тепер розгляньмо, який вигляд вона матиме, коли e дуже мале. Чисельник другого дробу в рівнянні (11) дорівнює (1 − e cosθ)2 = 1 − 2e cosθ + e2 cos2 θ, тому члени нульового та першого порядку в чисельнику та знаменнику цього дробу однакові, і різниця між чисельником та знаменником виявляється лише у членах, пропорційних e2. Рівняння (11), отже, дає бажаний результат – рівняння (1). Для трохи більшої визначеності ми можемо залишити в рівнянні (11) члени порядку e2:
(12)де O(e3) позначає члени, пропорційні e3 або вищим степеням e.
22. Фокусна відстань
Розгляньмо вертикальну скляну лінзу з опуклою поверхнею спереду та пласкою ззаду, схожу на ту, що її Ґалілей та Кеплер використовували в передній частині своїх телескопів. Криві поверхні, найзручніші для виточування та шліфування, є сегментами сфер, тож ми припускатимемо, що опукла передня сторона лінзи є сегментом сфери радіусом r. Ми також вважатимемо, що ця лінза тонка, тобто її максимальна товщина значно менша за r.
Припустімо, що якийсь промінь світла, який рухається в горизонтальному напрямку, паралельному осі лінзи, падає на лінзу в точці P, при цьому відрізок від центра кривини C (позаду лінзи) до точки P утворює з осьовою лінією лінзи кут θ (тета). Лінза заломить цей промінь світла так, що коли він вийде ззаду неї,
Увага!
Сайт зберігає кукі вашого браузера. Ви зможете в будь-який момент зробити закладку та продовжити читання книги «Пояснюючи світ», після закриття браузера.